International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 108

ISSN 2229-5518

A Combined Approximation to t-distribution

Naveen Kumar Boiroju, R. Ramakrishna

Abstract— In this paper, a simple function developed for computing probability values of t-statistics. This function corrects the function proposed by Gleason (2000) with good accuracy and also it provides comprehensive t-statistic probability values without further check of the statistical ta- bles. Probability values for any t-test statistic could be readily obtained from the suggested function and the proposed approximation guarantees

atleast three decimal point accuracy, which is more than sufficient to compare the probability value with the level of significance in statistical hy- pothesis testing.

Index Terms— t-distribution, CDF, Maximum absolute error.

1 INTRODUCTION

——————————  ——————————

T is common knowledge that the t-statistic plays a key role in statistics and is the mostly used statistic in the statistical infer- ence of a population mean or comparison of two population means. Therefore an accurate approximation to its cumulative distribution function (CDF) is very much needed in the statistical

hypothesis testing (Jing et al., 2004, Johnson et al., 1995). Two in-

develop a new approximation function to the CDF of t- distribution. In this paper, an improved function suggested by correcting the Gleason (2000) function, then a new combined ap- proximation discussed for 3 ≤ ν ≤ 30 and for all t ≥ 0 .

2 METHODS

dependent variables X and Y such that

X ~ N (0,1)and

It is well known that the t-distribution is symmetric distribution
and tends to follow normal distribution for large degrees of free-

Y ~ χ ( n )

respectively, the statistic

t = X /

(Y / n)

is said to
dom (say n>30). The case t<0 can be handled by symmetry proper-
have a t-distribution with n degrees of freedom. The probability
density function of t-distribution with ν degrees of freedom is
ty of the distribution. Gleason (2000) proposed two approxima- tions with two decimal point accuracy.
given by

F1 = Fν (t ) = F(Zν (t ))

(2)

f (t ) =

1

 1 ν 

1

ν +1

; − ∞ < t < ∞

(1)
where

F(.)is the CDF of standard normal distribution,

ν B , 

 2 2 



1 +

t 2  2



ln(1 + t 2

Z t

/ν )

ν − 1.5

 ν 

ν ( ) =

g (ν )

and

g (ν ) = (ν − 1)2 . (3)

There is no closed form to the CDF of t-distribution which show
the way to refer the cumbersome and insufficient statistical tables.
The second function defined by Gleason (2000) is given by substi-

ν − 1.5 − (0.1/ν ) + 0.5825 /ν 2

Hence, an approximation of CDF could provide the probability
values for a t-statistic and often plays a key role in statistical infer-
tuting

g ∗ (ν ) =

(ν − 1)2

in place of
ence. Recently, the approximations of t-distribution function dis- cussed by Yerukala et al. (2013) and their paper motivated us to

g (ν ) in equation (3).

ln(1 + t 2 /ν )

————————————————

F2 = Fν (t ) = F(Zν (t )) with Zν (t ) =

g ∗ ν

(4)

• Naveen Kumar Boiroju, Department of Statistics, Osmania University, Hyderabad, India. E-mail: nanibyrozu@gmail.com

• R. Ramakrishna, Vidya Jyothi Institute of Technology, Post, Aziznagar,

Hyderabad, India. E-mail: ramakrishnaraavi9292@gmail.com
We propose a better approximation function by subtracting a non-
linear component to the function F2 and the resulting function is given as

IJSER © 2014 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 109

ISSN 2229-5518

 7.9 +

 Atleast two decimal point accuracy is obtained at 3 and 4 degrees

F3 = Fν (t ) = F2 − [  / 10000]

7.9 tanh 3 − 0.63x − 0.52ν

of freedom for the functions F , F
and F
where as the function F

  1 2 3 4

9

where x = 

if t = 0

(5)
has the same accuracy for the degrees of freedom between 3 and

t otherwise

Li and Moor (1999) suggested a natural modification of the ordi- nary normal approximation to t-distribution.

F4 = Fν (t ) = F(Zν (t )) ,

5. The function F1 provides the three decimal point accuracy
when the degrees of freedom lie in between 5 and 12 whereas the functions F2 and F3 provide atleast three decimal point accuracy for the degrees of freedom lie in between 5 and 14. The function
F4 provides three decimal value accuracy for degrees freedom
where Zν

(t ) = t (4ν + t 2 − 1)/(4ν + 2t 2 )

(6)
from 6 to 11 whereas the function F5 gives the same accuracy for
A combined function defined based on the errors of these func- tions as
degrees of freedom from 3 to 9. The four decimal point accuracy for the function F1 is obtained for degrees of freedom from 13 to

F4 ;



5  3 ;

F1 ;

0 ≤ t <1.3 + 0.04ν

1.3 + 0.04ν ≤ t < 5.94 − 0.04ν

t ≥ 5.94 − 0.04ν

(7)
30, for the functions F2 and F3 , it is obtained for the degrees of freedom from 15 to 30. The function F4 gives four decimal point accuracy when the degrees of freedom from 12 to 21 whereas the
same is observed for the function F5 in between 10 to 21 degrees
The efficiency of these functions measured using the minimum of
maximum absolute error and the error is computed as the differ- ence between the probability of the given function and with that of the TDIST() function available in Microsoft office Excel 2007 software.

3 RESULTS AND DISCUSSION

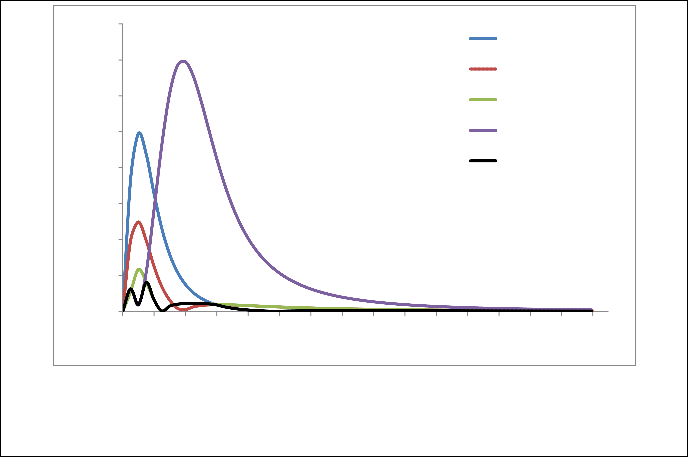
The maximum absolute error of these functions observed at 3 de- grees of freedom and the Figure 1 presents the absolute errors of the functions at 3 degrees of freedom. It is evident that the cor- rected function and combined function has lowest absolute errors as compared with other approximations. At 3 degrees of freedom, Function F 4 has the maximum absolute error 0.0069818 observed at t=3.8, function F1 has the maximum absolute error 0.0049514 observed at t=1 and the function F2 has the maximum absolute error 0.0025012 observed at t=0.9. The corrected function F 3 has the maximum absolute error 0.0011699 observed at t=1 and the combined function (F5 ) has the maximum absolute error
0.0008117 observed at t=1.5. The proposed combined function also accurate to the three decimal points as like of the functions de- fined in Yerukala et al. (2013). It is also observed that the pro-
posed functions performing well at the tail probabilities.
of freedom. Only two functions F4 and F5 provide the accuracy up to five decimal points when the degrees of freedom are greater than or equal to 22. From the Table 1, it is observed that the pro- posed combined function F5 , guaranty the three decimal point accuracy and it may be treated as a competitor for the functions proposed by Yerukala et al. (2013).

4 CONCLUSION

The proposed combined function (F5 ) guaranties the accuracy up to three decimal points to the CDF of t-distribution where as the corrected function F3 is the efficient function as compared with the other two functions at lower degrees of freedom (Table 1). The function F5 is better than the functions F1 , F2 , F3 and F4 for all ν ≤ 30 . The accuracy of F4 and F5 is almost equivalent for all
ν > 16 . The functions F1 and F2 are better than the function F4
for all ν < 8 and F1 is better than the functions F2 and F3 for all ν > 5 . The accuracy of the functions F2 and F3 are same for all ν > 11. The proposed two functions are guarantying the accura- cy up to three decimal points at the tails of the distribution and it
is more than sufficient in the testing of hypothesis using t-
statistics.

IJSER © 2014 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 110

ISSN 2229-5518

TABLE 1

Maximum absolute errors of the approximations

IJSER © 2014 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 111

ISSN 2229-5518

0.008

0.007

0.006

Gleason (2000)-F1

Gleason (2000)-F2

Corrected Function-F3

0.005

0.004

Li & Moor (1999)-F4

Combined Function-F5

0.003

0.002

0.001

0

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30

t

Fig. 1. Maximum absolute error of the approximations for 3 degrees of freedom

REFERENCES

[1] B.Y. Jing, Shao, Q.M. and Zhou, W. Saddle- point approximation for student’s t-statistic with no moment conditions, The Annals of Sta- tistics, 32 (6), pp2679-2711, 2004.

[2] N.L. Johnson, Kotz, S. and Balakrishnan, N., Distributions in Statistics: Continuous Univariate Distributions, Vol. 2, Second edition, New York. Wiley, 1995.

[3] R. Yerukala, Boiroju, N.K. and Reddy, M.K., Approximations to the t-distribution, Interna- tional Journal of Statistika and Mathematika, Vol.

8 (1), pp19-21, 2013.

[4] J.R. Gleason, A note on a proposed student t approximation, Computational Statistics & Data

Analysis, 34, pp63-66, 2000.

[5] B. Li and Moor, B.D., A corrected normal ap- proximation for the Student’s t distribution, Computational Statistics & Data Analysis, 29, pp213-216, 1999.

IJSER © 2014 http://www.ijser.org