International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 1

ISSN 2229-5518

Robust Control of Inverted Pendulum Using Fuzzy Sliding Mode Control and Particle Swarm Optimization “PSO” Algorithm

Assef Zare Assistant Professor Islamic Azad University

,Gonabad Branch, Iran asefzare@yahoo.com

Toktam Lotfi

MSC Student Islamic Azad University, Gonabad Branch, Iran Aylinlotfi@yahoo.com

Hodeiseh Gordan

MSC Student Islamic Azad University, Gonabad Branch, Iran
hodeisehgordan@gmail.com

MohamadReza Dastranj

MSC Student
Islamic Azad University ,Gonabad Branch, Iran mohamadrezadastranj@gmail.com

Abstract—One of the most important problems today is robotics and its control , due to the vast Application of inverted pendulum in robots. In this paper, we have tired to optimally PID Controller inverted pendulum using PSO Algorithm by nonlinear equations. The results of this simulation has been mentioned in the conclusion. It seems that the results be acceptable results.

Keywords-nonlinear;optimal; Sliding Mode; PSO algorithm; Inverted Pendulum

For this example, let's assume that

TABLE I. PHYSICAL PARAMETERS OF INVERTED PENDULUM

I. INTRODUCTION

An inverted pendulium is inherently unstable, and must be actively balanced in order to remain upright, by moving the pivot point horizontally as part of a feedback system. There are variety methods for inverted pendulium control that are presented since now. The presented methods for inverted penduliums control are divided generally in three groups. Classic methods such as PID, PI controllers [1,

2].Modern methods (adaptation-optimum) [3,4,5]. Artificial methods such as neural networks and fuzzy [6, 7].theory are
the presented methods for inverted pendulium angle control.
The design method in linear control comprise based on main application the wide span ' of frequency, linear controller has a weak application, because it can't
compensate the nonlinear system effect completely.
II. MODELING AN INVERTED PENDULUM

The cart with an inverted pendulum, shown below, is "bumped" with an impulse force, F. Determine the dynamic equations of motion for the system, and linearize about the pendulum's angle, theta = 0 (in other words, assume that pendulum does not move more than a few degrees away from the vertical, chosen to be at an angle of 0). Find a controller to satisfy all of the design requirements given below.
.
.
This system is tricky to model in Simulink because of the physical constraint (the pin joint) between the cart and pendulum which reduces the degrees of freedom in the system. Both the cart and the pendulum have one degree of freedom (X and theta, respectively). We will then model Newton's equation for these two degrees of freedom.




∑ ( ) (1)



∑ ( ( ) ( )) ( )
It is necessary, however, to include the interaction forces N and P between the cart and the pendulum in order to model the dynamics. The inclusion of these forces requires modeling the x and y dynamics of the pendulum in addition to its theta dynamics. Generally, we would like to exploit the modeling power of Simulink and let the simulation take care of the algebra. Therefore, we will model the additional x and y equations for the pendulum.

∑ (3)

(4)

Figure 1.The structure of an Inverted Pendulum

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 2

ISSN 2229-5518

( )

( ) ( )
However, xp and yp are exact functions of theta. Therefore, we can represent their derivatives in terms of the derivatives of theta.
( ) (7)



( ) ( )




( ) ( ) ( ) ( )
( ) (10)


( ) ( )



( ) ( ) ( ) ( )
These expressions can then be substituted into the
expressions for N and P. Rather than continuing with algebra here, we will simply represent these equations in Simulink.
Simulink can work directly with nonlinear equations, so it is unnecessary to linearize these equations.

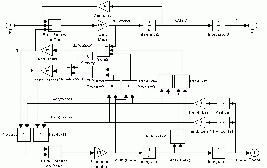
Figure 2.The block diagram of an Inverted Pendulum

III. SLIDING MODE CONTROLLER Nonlinear system control that its model isn't clear carefully
works with tow methods: (1)Robust control methods. (2)adaptive control methods.
In control view, uncertainly in modeling is divided in two main kinds:
(1).Non certainly in existent Para meters in model
(2).Estimating the lower step for system and being UN
modeled dynamics in the estimating model.
Sliding control is one of the designed modes for robust control that make access to system desired application estimating system in model.
The major idea of this method is the controlling of nonlinear first grade system is easier than n grade system control in spite of uncertainly.
But this function maybe cause the control law with more energy that is not practicable implement tat ion.
Sliding mode is really compromise between modeling and suitable operation with inaccurate design.
We consider the non linear system model in this rule:
( ) ( ) ( )
That F(x) is nonlinear function, its high boundary
characterized as X function.
B(x) is a continuous function that its high and low boundaries characterized by X function.
The good of finding X is in this way that in g(x)F(x) function we can follow the desirable mode in spite of uncertainly.
̃[̃ ̃ ̃ ] ( )
In ideal state
̃(15)
Sliding surface equation defines as below:
∫ ( )
Because of the signals of control that gain with this
designing method has limited energy, it is necessary to:
( ) ( ) ( )
in other word:
( ) ( )

| | ( )
in designing, the control low on S(t) continuously is noticed
cause we should concentrate to carelessness in model in sliding surface and reduced the chattering effect.
We can write the system's dynamics when in some situation they are in sliding state.
S'=0 (20)
The gained control signals for this system are as below:
( )

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 3

ISSN 2229-5518

K- 1 s

Pulse

Generator

Subsystem

Gain Integrator

du/dt

f teta

0

Constant

-K- Gain1

du/dt

Derivative

Derivative1

Saturation1

Fuzzy Logic

Controller with Ruleviewer

-K- Gain2

Product1

Scope

Figure 3.simulink block diagram of FSMC

Figure 6.Membership functions for (out fuzzy)

normalized outputs

Fuzzy controls are designed based on created sliding surface and sliding surface changes.
All of the fuzzy rules collection came in Table II

TABLE II. FUZZY RULE

Figure 4.Membership functions for (s) normalized inputs

Figure 5.Membership functions for (ds/dt)

normalized inputs

IV. PARTICLE SWARM OPTIMIZATION (PSO) ALGORITHM
Since the introduction of the particle swarm optimizer by James Kennedy and Russ Eberhart in 1995 [9],numerous variations of the basic algorithm have been developed in the literature. Each researcher seems to have a favorite implementation - different population sizes, different neighborhood sizes, and so forth. In this paper we examine a variety of these choices with the goal of defining a canonical particle swarm optimizer, that is, an off-the shelf algorithm to be used as a good starting point for applying PSO.The original PSO formulae defined each particle as a potential solution to a problem in D-dimensional space,with particle i represented Xi=(xi1,xi2,...,xiD). Each particle also maintains a memory of its previous best position, Pi=(pi1,pi2,...,piD), and a velocity along each dimension, represented as Vi=(vi1,vi2,...,viD). At each iteration, the P vector of the particle with the best fitness in the local neighborhood, designated g, and the P vector of the current particle are combined to adjust the velocity along each dimension, and that velocity is then used to compute a new position for the particle. The portion of the adjustment to the velocity influenced by the individual’s previous best position (P) is considered the cognition component, and the portion influenced by the best in the neighborhood is the social component [10,11].
In Kennedy’s early versions of the algorithm, these
formulae are:
( ) (
) ( )
( )
Constants j1 and j2 determine the relative influence of the social and cognition components, and are often both set to the same value to give each component (the cognition and social learning rates ) equal weight. Angeline, in[1], calls this the learning rate. A constant, Vmax, was used to

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 4

ISSN 2229-5518

arbitrarily limit the velocities of the particles and improve the resolution of the search.
In [9] Eberhart and Shi show that PSO searches wide areas effectively, but tends to lack local search precision.
Their solution in that paper was to introduce w, an inertia factor, that dynamically adjusted the velocity over time, gradually focusing the PSO into a local search:
( )
( ) ( )
V. SIMULATION
We want to determine control coefficients "sliding mode control" for an Inverted Pendulum by using of "PSO" algorithm in this paper. we consider "PSO" three variable for a1 & a2. Every of three variable are different at number of first population with first situation and speed."PSO" algorithm defined the situation of a1 & a2 and applying to simulation models. Then was receipted two output of it first output is maximum of overshot system and second output is error and is organized ,Current_fitness function as following.
(25)
For all of the population calculate current_fitness function , after formatting current _fitness, we should determine global
_best_ Fitness according below.
( ) (26)
At duration by notice to fitness position of individual best must be determined. With "PSO" adjustment parameters we can obtain optimal answers good. The process of updating in speed and situation is according equation(6,7).The result of simulation for 50 population and number of process of flying for 50 times are good results. That is shown at the end of the paper.

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

VI. CONCLUSION
In this paper, a robust control system with the fuzzy sliding mode controller and the additional compensator is presented for a Inverted Pendulum position control. According to the simulation results, the FSMC controllers can provide the properties of insensitivity and robustness to uncertainties and external disturbances, and response of the Inverted Pendulum for FSMC controllers against uncertainties and external disturbance is the same Fuzzy sliding mode controller gives a better response to system than the fuzzy and classical PID controllers . if control parameters set suitably.
REFERENCES

[1].JIA Nuo, WANG Hui. Nonlinear Control of an InvertedPendulum System based on Slinding mode method. ACTA Analysis Functionalis applicata, 2008,9(3): pp.234-237.

[2].O. Tolga Altinoz, A. Egemen Yilmaz, Gerhard Wilhelm Weber Chaos Particle Swarm Optimized PID Controller for the Inverted Pendulum System 2nd International Conference on Engineering ptimization September 6-9, 2010, Lisbon, Portugal.

[3].Wu Wang Adaptive Fuzzy Sliding Mode Control for Inverted Pendulum Proceedings of the Second Symposium International Computer Science and Computational Technology(ISCSCT ’09) uangshan, P. R. China, 26-28,Dec. 2009, pp. 231-234.

[4].Viroch Sukontanakarn and Manukid Parnichkun, “ Real-Time Optimal Control for Rotary Inverted Pendulum, ”American Journal of Applied Sciences 6 (6): 1106-1115, 2009 ISSN 1546-9239 © 2009 Science Publications.

[5].Alexander Bogdanov Optimal Control of a Double Inverted Pendulum on a Cart Technical Report CSE-04-006 December 2004.

[6].T. Sugie, and K. Fujimoto, “Controller design for an inverted pendulum based on approximate linearization,” Int. J. of robust and nonlinear control, vol. 8, no 7, pp. 585-597, 1998.

[7]Shin-ichi Horikawa, Masahiro Yamaguchi, Takeshi Fuzzy Control for

Inverted Pendulum Using Fuzzy Neural Networks January 10, 1995.

[8].Zadeh, I.H. and S. Mobayen, “ PSO-based controller for balancing

rotary inverted pendulum, ” J.AppliedSci.,16:2907-2912 2008.

[9].J. Lam, “Control of an Inverted Pendulum”, University of California, Santa Barbara, 10 June 2004 Yasar Beceriklia,_,1, B. Koray Celikb Fuzzy control of inverted pendulum and concept of stability using Java application Mathematical and Computer Modelling 46 (2007) 24–37

0.6

0.5

0.4

0.3

0.2

0.1

0

-0.1

0 1 2 3 4 5 6 7 8 9 10

Time(s)

-0.1

0 1 2 3 4 5 6 7 8 9 10

Time(s)

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 5

ISSN 2229-5518

Figure7.Inverted pendulum rod angle for initial 0.7 radians(BestResult) Figure8.Inverted pendulum rod angle for initial 0.5 radians(BestResult)

IJSER ©2012 http:IIWWW.IISerorq