
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1840
ISSN 2229-5518
Graph Coloring Algorithm using Adjacency
Matrices
M Saqib Nawaz1, M Fayyaz Awan2
Abstract- Graph coloring proved to be a classical problem of NP complete and computation of chromatic number is NP hard also. Graph coloring with 2 colors exhibits polynomial time behavior whereas optimal solution for whether a graph is colorable for k >2 is NP-complete. An algorithm for graph coloring is proposed in this paper. Algorithm uses adjacency matrix for coloring the vertices of given undirected graphs.
Index Terms— Adjacency matrix, Chromatic number, Graph coloring, NP, Polynomial time, Vertices.
—————————— ——————————
RAPH coloring is an interesting and challenging problem in graph theory. Graph coloring is an assignment of a
‘color’ to the elements of graph. In vertex coloring, each vertex of the graph is colored such that no two adjacent verti- ces has the same color. In edge coloring, each adjacent edge is colored with different color. Problem of graph coloring is de- ceptively simple. The main idea of coloring a graph is straight- forward, and it seems that graph coloring is an easy problem, but it is not. A simple algorithm for graph coloring is easy to describe, but potentially extremely expensive to run. Graph coloring problem is known to be NP-complete [1]. Problems are either classified in P, NP or NP-Complete (NPC) classes [8]. Class P consists of those problems that are solvable in pol- ynomial time. NP class consist of those problems that are veri- fiable in polynomial time. Any problem that belongs to P also belongs to NP. A decision problem X’ is said to be NP- complete if X’ is in the set of NP problems and also in the set of NP-hard problems. The abbreviation NP refers to "nondeterministic polynomial time."
There is no known algorithm which will color optimally all the vertices of the graph for every graph in polynomial time. Optimal solution to graph coloring problem may be found by determining minimal colorings for the corresponding graphs. Unfortunately, this may not always be achieved in a reasona- ble amount of time.
The chromatic number of a graph is the least number of col- ors needed for coloring the graph and is often denoted χ(G). A graph is k-colorable if graph can be assigned a k-coloring, and graph is k-chromatic if graph chromatic number is exactly k. If χ(G) = 2 then graph is bipartite. Chromatic polynomial can be defined as a function P(G, k) that counts the number of k- colorings of G. For a given graph this function is polynomial in k. With chromatic polynomial, chromatic number χ(G) is the smallest integer (positive) that is not a root of the chro- matic polynomial.
————————————————
2 M Fayyaz Awan is currently pursuing MS degree program in Computer
Science in University of Sargodha, Pakistan. E-mail: uos_pk@yahoo.com.
χ(G) = min{k: P(G,K) > 0 }.
The problem of finding the chromatic number and a prop- er coloring of a graph is of great interest for its widespread applications in areas such as scheduling and timetabling and particularly in telecommunications. Algorithm which is de- scribed in this paper uses adjacency matrix for vertex coloring of a graph.
A graph G is k-colorable if it can be colored using k or fewer colors. Task of closely approximating the chromatic number of a graph is NP-complete [5] and thus virtually impossible to accomplish for large graphs. Consequently, approximations of upper and lower bound results established for χ (G) have gen- erally been crude and of little practical use [1, 6]. Polynomial time algorithm to determine whether a graph is 2-colorable or not is discussed in this section along with greedy algorithm which is an approximation to optimal solution.
Efficient and simple algorithm exist that determines whether a graph is 2-colorable and if a graph can be colored with two colors then this algorithm assigns colors to its vertices on breadth-first search basis. Assign suppose ‘blue’ to the first layer, ‘red’ to the second layer, ‘blue’ to the third layer, etc. Go over all the edges and check whether the two end points of this edge have different colors. Algorithm time complexity is O(|V|+|E|). The last step is used for correctness of the algo- rithm. However for k > 2, the problem is more difficult. Whether a given graph is k-colorable for k > 2 is an NP- complete problem. The first algorithm that can be thought of is brute-force search where every possible assignment of k colors to the vertices is considered, and check whether any of them are correct. This is done in the order of O((n+1)! so impractical to use. Therefore an optimistic algorithm is required for graph coloring.
Greedy algorithm does not give the lowest k for which there
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & En1841gineering Research, Volume 4, Issue 4, April-2013 1841
ISSN 2229-5518
exists a k-coloring, instead it tries to find a reasonable coloring while still being reasonably expensive. Greedy algorithms are also known as an approximation algorithm because some reasonable solution is fined in greedy algorithm. Greedy algorithm proceeds as follows: Consider the vertices to be in a specific order v1,...,vn and assign to vi the smallest available color not used by vi's neighbors among v1,...,vi − 1, adding a fresh color if needed. This algorithm finds a reasonable coloring and is O (|V|+|E|). Problem with greedy algorithm is that it does not find the optimal k for which the graph is k- colorable. In some cases, k can be as high as n/2 when the optimal k would be 2. Figure 1 shows this. In figure 1 the left ordering leads to a using only 2 colors, and the right ordering leads to 4 colors.
Figure 1. Coloring with left and right ordering
Graph G with vertices (nodes) V and edges E is denoted by G(V, E). The adjacency matrix also called as connection matrix for a graph with ‘n’ vertices is an n×n matrix whose (i, j) entry is 1 if the ith vertex and jth vertex are connected, and 0 if they are not [2]. For a simple graph with no self-loops, the adjacen- cy matrix must have 0’s on the diagonal. For an undirected graph, the adjacency matrix is symmetric.
Figure 2. Adjacency matrix of a graph.
Neighbor vertices are those vertices that are connected to a specific vertex whereas non-neighbor are those vertices that are not connected to a specific vertex. In figure 2, vertex A is
not connected with vertex C, D, E and F. It can be seen in ma- trix as in first row column third (vertex C), column fourth (vertex D), column fifth (vertex E) and column six (vertex F) values are 0. Vertex C, D, E and F are the non-neighbors (NN) of vertex A whereas vertex B is the neighbor of vertex A. De- gree of a vertex denoted by d(W) is the number of edges con- nected to a vertex W or the number of vertices connected to the Vertex (W). A coloring of G is mapping function f: V→ {1,
2,…., k} such that f(u)= f(v) if and only if (u, v) Ɛ E. Vertex A degree in above figure is 1 and vertex with maximum degree is vertex B and F whereas vertex D has minimum degree.
Proposed algorithm uses adjacency matrix to color a graph G with V vertices and E edges. G is considered to be an undi- rected graph. Through adjacency matrix, each vertex neigh- bors and non-neighbors are found with degree of each vertex. Algorithm proceeds as follows:
Given G(V, E), make an adjacency matrix of the G. Compute degrees of each vertex and assign color 1 to vertex that has maximal degree in G, say X. Assign same color to the non- neighbor (NN) say Y of X. Find the common vertices of X and Y and if these common vertices are not adjacent then assign them color 2, else assign them different colors. Now take the new NN of X, if this new NN is adjacent to the previous NN or to any colored vertex then color this vertex with different color. Color common and NN vertices with previous colors such that no two adjacent vertices has the same color. If previ- ous used color violates the rule of graph coloring then assign a new color. Repeat this until non-colored vertices equals zero.
Given a Graph G(V,E):
1. Calculate total vertices n in G.
2. Make an adjacency matrix of n×n matrix.
3. Calculate the degree of each node using matrix obtained in step 2.
4. Select the maximum degree node suppose X. Color X
and its NN suppose Y with same color.
5. If X and Y has common vertices then color it with color different then X.
6. If common vertices of step 5 are not adjacent then color these vertices with same color.
else color these vertices with different color.
7. If X has other new neighbor then go to step 8
else take new NN as the NN of Y and go to step 8.
8. If new NN and previous NN are adjacent then color new
NN with different color other then X. else color new NN with color of X.
9. If new NN is adjacent to any colored vertices or to any previous NN then color it with different color.
10. Until non-colored vertices > 1, go to step 5.
11. return G.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & En1842gineering Research, Volume 4, Issue 4, April-2013 1842
ISSN 2229-5518
Algorithm proposed here is applied on the graph shown in figure 3.
Figure 3. Graph with seven vertices.
Graph is undirected and it has seven vertices. So its adja- cency matrix will be of order 7 × 7.
M =
Integer number represents color. 1 represent color red, 2 represent blue, 3 represent color yellow, 4 color green and so on. Maximum degree vertex is A. NN of vertex A is vertex D. Algorithm will assign color suppose 1 to vertex A and D. Common vertices of vertex A and D are vertex B, C and E and vertex E is adjacent to both B and C, so B and C will get color 2 and E will get color 3. Second NN of vertex A is vertex G and G is adjacent to previous NN D and colored vertex B. Assign vertex E color to vertex G that is 3. Vertex F is the common vertex in A and new NN vertex G. F is adjacent to both vertex A and C so assign new color 4 to vertex F. So vertex A and D are red colored, vertex B and C are blue colored, vertex G and E are yellow colored and vertex F is green colored. Each vetex is colored so that it is not adjacent to any same color vertex. Graph with coloring is shown below. Graph is colored with four different colors.
Graph coloring along with classes of P and NP problems are an active field of research. Algorithm presented here works well for graph coloring and algorithm is based entirely on ad- jacency matrix for coloring, but still a lot of improvements can be done. Proposed algorithm lacks correctness proof. Algo- rithm along with correctness proof is implementable in Matlab.
The authors wish to thank Dr. Khalid Amir for his generous time and help in in paper preparation.
[1] Aho, A. V., Hopcroft, 1. E., and Ullman, J. D., The Design and Analysis 0f
Computer Algorithms, (Addison-Wesley, Reading, MA, 1974), pp. 364--404.
[2] Chartrand, G. Introductory Graph Theory. New York: Dover, p. 218,
1985.
[3] J.A. Bondy and S.C. Locke. Largest bipartite subgraph in triangle-free graphs with maximum degree three",J. Graph Theory, vol. 10, pp. 477-504, 1986.
[4] Leighton, F. T. A Graph Coloring Algorithm for Large Scheduling Problems., Journal of Research of the National Bureau of Standards Vol. 84, No.6, No- vember-December 1979.
[5] Garey, M. R., and Johnson, D. S., The Complexity of Near-optimal Graph
Coloring, Journal of the ACM, Vol. 23, No.1 (Jan. 1976), pp. 43-9.
[6] Christofides, N., Graph Theory-An Algorithmic Approach, (Academic Press, New York, 1975), pp. 58-78.
[7] Matula, D. W., Marble, G., and Isaacson, J. D., Graph Coloring Algorithms, Graph Theory ami Computing, Ronald C. Read, editor, (Academic Press, New York, 1972), pp. 109-122.
[8] Cormen, T. H., Leiserson C. E., Rivest R. L., and Stein, C., Introduction to
Algorithms, 3rd edition. 2009.
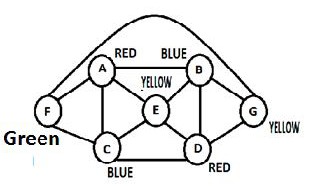
Figure 4. Vertex colored graph (1)
IJSER © 2013 http://www.ijser.org