International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 1

ISSN 2229-5518

A Simple Bird’s Eye View

Transformation Technique

M.Venkatesh, P.Vijayakumar

Abstract—Bird’s Eye View transformation technique is to generate a top view perspective of an image. Now a days machine vision is one of the hottest area under research for extracting information from images. By implementing bird’s eye view transformation technique we increase the scope of extracting information from images. Different perspective view is one of the key requirements in W SN image based monitoring s ystems. This paper discusses a simple perspective transform technique to generate a Bird’s Eye View. We discuss a technique were we can generate a bird’s eye view by using a simple pin hole camera model. To develop a real time product and evaluate real time performance of this technique, we implemented it on a 32- bit floating point VLIW TMS320C6713 DSP processor.

Index Terms— top view transform, perspective transform, geometrical image transformation, camera imaging model, bird’s eye view car parkin g system, digital image processing.

1 INTRODUCTION

——————————  ——————————

IRD’S Eye View transformation technique is to generate a top view perspective of an image as shown in Fig. 1.
This technique can be classified under digital image
processing as geometrical image modification. Basically the
bird’s eye view transform can be divided into three steps
.First we have to represent the image in a shifted coordinate
system, next perform rotation of image, and then project the image on a two dimensional plane. The block diagram for transformation is given in Fig. 2.

Image in general is represented as two dimensional matrix, where each location represents a pixel value which is between 0 to 255 (for a 8-bit grayscale image). We are interested in the location of each pixel which will be basically relocated to a new position.

Fig. 1. Bird’s eye view transform

Fig. 3. Change in pixel position

2 COORDINATE SHIFTING

Image is generally represented as two dimensional plane i.e. x and y plane. So if the size of an image is 100 
100 then each pixel location is represented as shown in
Fig. 4.
To perform rotation of image first we need to apply a change in coordinate position such that the image centre is located at (0, 0), thus in a 100  100 image starting point is (-50, -50) and ending point at (49, 49) as shown in Fig. 5.
If (x, y) represent the coordinates of an image then shifted coordinate is given by (X, Y) as shown in (1) and (2).

X = x - (IMAGE SIZE / 2) (1) Y = y - (IMAGE SIZE / 2) (2)

Fig. 2 Block Diagram

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 2

ISSN 2229-5518

0 0 0 1

(4)

1 0 0 0

Ry = 0 cos � sin(�) 0

(5)

0 −�𝑖�(�)

0 0

cos(�) 0

0 1

Fig. 4. Representation of image pixel locations

Rz =

(6)

Fig. 5. Coordinate change of input image

If the camera is mounted at 450 angle to ground and we try to rotate the image by 450 then what we get is the top view of the given image as shown in Fig. 6. Hence our technique generate a bird’s eye view transform based on manual observation or by knowing the angle at which camera is mounted, this process can also be automated by techniques represented in [6]. After rotation is performed the height of the image decreases hence we need to stretch the height of the image, which is done by using matrix SH as in (7). If Sx = 2 then the height will become twice that of original.

3 ROTATION AND SCALING OF AN IMAGE

The rotation of an image can be performed by simple matrix multiplication operation, if (X, Y, Z) is the location of the pixel in input image then (p, q, r) represents the location for the rotated image. The Z is introduced as

SH =

(7)

third coordinate, representing the image in three
dimensions (3D). The initial value of Z can be assigned as zero for each pixel change followed by projection operation. The mathematical representation of rotation operation is given by (3).
We can combine (6) and (7) to get a single equation for
bird’s eye view transform matrix B as given by (8).

� �

� = R �

� �

1 1

(3)

Where R is 4x4 rotation matrix [1]. We can perform rotation around x, y and z axis by using different rotation
matrix given by (4), (5) and (6). Where Θ, α and β are the
angles for rotation. Bird’s eye view transform is given by
Rz matrix.

Fig. 6. Rotation of image on z – axis

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 3

ISSN 2229-5518

Fig. 7 Projection into a 2D image plane

𝑆�(𝑐�� ) 0 − sin � 0

5 EXPERIMENTAL RESULTS

For embedded based applications we implemented the technique on TMS320C6713 DSP Starter Kit (DSK) developed jointly with Spectrum Digital is a low-cost development platform. The kit uses USB communications for true plug-and-play functionality. Code Composer Studio IDE is used where the code is written in simple C language. We got the following results on DSK as shown in Fig. 8 and Fig. 9. For different size of the image, the time required for processing has been calculated as shown in table (1). So if a video has to be generated for about 15 frames /sec then it would require processing time to be around 0.066s per frame. Hence a real time video can be generated by using an image size of 100 x
100 or less. For larger image size we would require a

B = 0 𝑆� 0 0

(8)

higher clock processor.

sin⁡(�)

0 cos � 0

0 0 1

TABLE 1

TIME COMPLEXION ANALYSIS

So the final equation that we get is given by (9).

� �

� = B �

� �

1 1

(9)

4 PROJECTION OF IMAGE ON TWO DIMENSIONAL

PLANE

The image has to be again represented in 2D plane for which the image has to be projected from the 3D plane to
2D plane like a simple pin hole camera model [1].
A simple projection formula can be written using similar triangles, where (p, q, r) are the positional coordinates in 3D plane and (u, v) are the output image coordinates as shown in (10) and (11). Here f represents focal length according to simple pin hole camera model. Focal length can have any arbitrary value.

6 CONCLUSION

We conclude that the technique is practical feasible technique and can be applied to different applications. This technique applies a simple rotation operation and

u = f p

f − r

v = f q

𝑓 − �

+ (IMAGE SIZE / 2) 10)

+ (IMAGE SIZE / 2) (11)

follows a simple pin hole camera model technique, hence requires a very low processing time hence can be applied for low cost application products.
In future we would like to show applications based on
The positional coordinate of the output image will have integer values hence the coordinate shifting is applied to get the coordinates in whole number.
this technique and further reduce the computation cost.

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 4

ISSN 2229-5518

Fig. 8. Bird’s Eye View Transform performed on DSK kit

REFERENCES

[1] “Digital Image Processing” fourth edition, William K. Pratt

2010 pp. 387-410

[2] LinBo Luo, InSung Koh, SangYoon Park, ReSen Ahn, JongWha

Chong “A software-hardware cooperative implementation of

bird’s-eye view system for camera-on-vehicle” IC-NIDC 2009

[3] Lin-Bo Luo, In-Sung Koh, Kyeong-Yuk Min, Jun Wang, Jong-

Wha Chong “Low-cost Implementation of Bird’s-eye View

System for Camera-on-vehicle.” 2010 IEEE

[4] H. Kano, Keisuke Asari, Yohei Ishii, Hitoshi Hongo “Precise top view image generation without global metric information,” IEICE Trans. Inf. & Syst., vol. E91-D, pp. 1893-1898, 2008.

[5] Yi-Yuan Chen, Yuan-Yao Tut, Cheng-Hsiang Chiul , and Yong- Sheng Chent “An Embedded System for Vehicle Surrounding Monitoring” 2nd International Conference on Power Electronics and Intelligent Transportation System 2009

[6] L. Jagannathan and C.V Jawahar “Perspective Correction

Method For Camera-Based Document Analysis ”

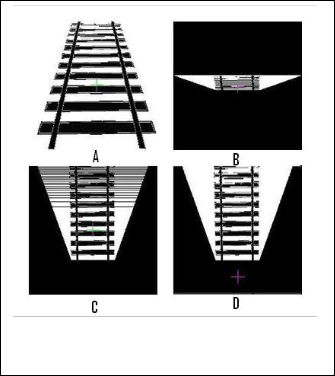
Fig. 9. Input image (A), Transformation with Θ = 80, S x = 1 (B), Transformation with Θ = 80, Sx = 8 (C), Output image after filling gaps (D)

http://www.ijser.org